We explain what the Pythagorean theorem is, how it is formulated and explained. Also, what are its characteristics, uses, and examples?
What is the Pythagorean Theorem?
The Pythagorean Theorem is a mathematical postulate made by the Greek philosopher and mathematician Pythagoras of Psalms (c. 569 - c. 475 BC), a student of the laws of mathematics whose contributions to arithmetic and geometry persist to this day in day. This postulate says that the sum of the square of the legs of a right triangle is always equal to the square of its hypotenuse.
This proposition is, without a doubt, one of the best known in the history of mathematics, and the one that has the greatest number of proofs over time, through different methods and elaborated by various philosophers and mathematicians.
According to some authors, up to a thousand different proofs can be found, although 367 have been formally cataloged. This is because the proof of the theorem was a requirement during the Middle Ages to achieve the title of Magister Matheseos (“Mathematician Teacher”) in the academy.
History of the Pythagorean Theorem
There is evidence of the Pythagorean Theorem on ancient Egyptian papyri.
Although the authorship of the theorem is attributed to the Greek Pythagoras, since his proof was of capital importance for the Pythagorean philosophers (disciples formed in an almost religious cult of mathematics), the truth is that the origin of this theorem is much earlier.
There is evidence of its use in Babylonian tablets and papyri from Ancient Egypt, but no document exposing their relationship is preserved to this day. It is known that the study of triangles was central to many of the ancient cultures.
Basic precepts of the Pythagorean Theorem
To begin with the Pythagorean theorem, it must be understood that the legs of a right triangle that form the right angle (90 °) are called the legs, and the remaining and longest side is called the hypotenuse.
Pythagorean Theorem Formula
The Pythagorean theorem is formulated as follows: a 2 + b 2 = c 2 where a and b are the legs of a right triangle and where c is its hypotenuse. From this formulation three corollaries or subsequent formulations are derived, of practical application and algebraic verification:
- a = ? c 2 - b 2 ( a is equal to the square root of c squared minus b squared)
- b = ?b 2 - a 2 ( b equals the square root of c squared minus a squared)
- c = ?a 2 + b 2 ( c is equal to the square root of a squared plus b squared)
Explanation of the Pythagorean Theorem
The Pythagorean Theorem allows you to calculate the sides of a triangle.
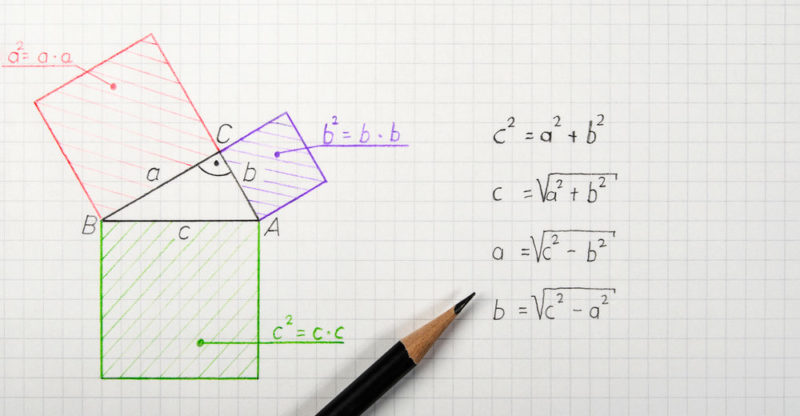
The logic of the Pythagorean theorem is quite simple and self-evident. Given a triangle with sides a, b, and c, in which a and b form a right angle (that is, 90 °), it is possible to calculate the length of the hypotenuse by adding the squares of the legs, or, any of the sides of the triangle.
Pythagorean Theorem Example
A simple example of applying the theorem is as follows:
- Given a right triangle whose legs a and b measure 3 and 4 cm respectively, we can calculate its hypotenuse c by substituting the values in the formula, as follows:
c 2 = a 2 + b 2
then c 2 = 3 2 + 4 2
and therefore c2 = 9 + 16 = 25
and finally c = ? 25 = 5
The hypotenuse c is 5 cm
Proofs of the Pythagorean Theorem
The Pythagorean Theorem has multiple proofs.
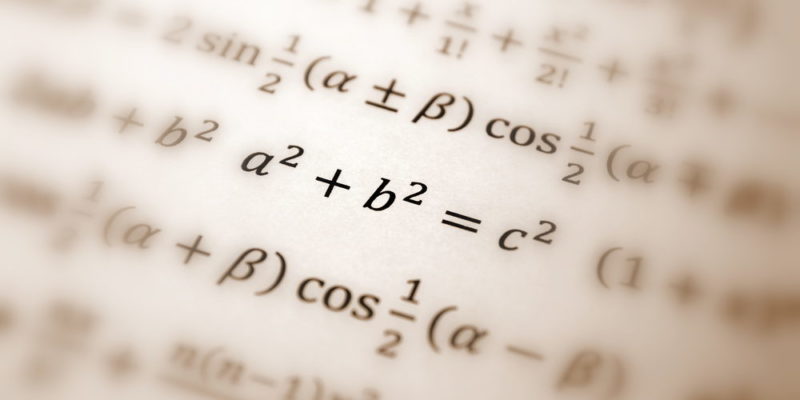
The proofs of the Pythagorean theorem are as varied as they are numerous, but those proposed by Euclid (325-265 BC), Pappus of Alexandria (290-350 BC), Bhaskara II of India (114-1185 AD), Leonardo da Vinci (1452-1519 AD) and James Garfield (1831-1881).
Each used different geometric and arithmetic methods that, however, always led to the same confirmation of the theorem.
Reciprocal proof of the Pythagorean Theorem
It is possible to use this theorem in its inverse sense, to check whether a given triangle is right (in cases, for example, where it cannot be graphed).
This is extremely simple: if in any triangle it turns out to be true that the sum of the square of its legs is equal to the square of the hypotenuse, then necessarily the first two will form a right angle and we will be in the presence of a right triangle.
Applications of the Pythagorean Theorem
The Egyptian pyramids fulfill many principles of the Pythagorean Theorem.
The applications of this theorem are numerous in the field of engineering, architecture, and geometry in general. Since ancient times the study of the triangle for practical purposes yielded tangible fruits, such as the famous pyramids of Egypt.
Any calculation situation in which we are in the presence of a right triangle will allow the application of this theorem to calculate any of its sides.
Importance for other areas
Other areas of mathematics can use this theorem for their calculations. For example:
- Plane analytical geometry. This theorem is used to find the distance between points on a Cartesian plane.
- Trigonometry. This theorem is used to prove the fundamental identity sin2 a + cos2 a = 1.
Exercises on the Pythagorean Theorem
Here are two exercises in this regard:
- Given the hypotenuse of 20 cm in a right triangle of which it is also known that one of its legs is 5 cm, how long will the remaining leg be?
- If a ramp needs to be made on a stair rung and it is known that the height of the rung is 30 cm and the length of the rung is 1 m, how much should the inclined plane of the ramp measure?
The above content published at Collaborative Research Group is for informational and educational purposes only and has been developed by referring to reliable sources and recommendations from technology experts. We do not have any contact with official entities nor do we intend to replace the information that they emit.
