The real numbers are the set that includes the natural, integer, rational and irrational numbers . It is represented by the letter ?.
The word real is used to distinguish these numbers from the imaginary number i , which is equal to the square root of -1, or ?-1. This expression is used to simplify the mathematical interpretation of effects such as electrical phenomena.
Characteristics of real numbers
In addition to the particular characteristics of each set that makes up the superset of real numbers, we mention the following characteristics.
Order
All real numbers have an order:
![]()
![]()
In the case of fractions and decimals:
![]()
![]()
Integral
The integrity characteristic of real numbers is that there are no empty spaces in this set of numbers. This means that each set that has an upper limit has a smaller limit.
Infinitude
Irrational and rational numbers are infinitely numerous, that is, they have no end, either on the positive or negative side.
Decimal expansion
A real number is a quantity that can be expressed as an infinite decimal expansion. They are used in measurements of continuous quantities, such as length and time.Each real number can be written as a decimal. Irrational numbers have endless and unrepeatable decimal places, for example, the number pi ? is approximately 3.14159265358979 ...
Classification of real numbers
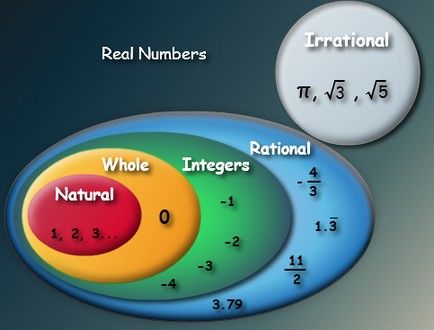
Natural numbers
Natural numbers arose from the need to count objects. These are the numbers we are most comfortable with: 1, 2, 3, 4, 5, 6, ... to infinity. The set of natural numbers is designated by the capital letter N .All numbers are represented by the ten symbols: 0, 1, 2, 3, 4, 5, 6. 7, 8, and 9, which are called digits .
Example
Natural numbers help us to tell how many classmates we have in class, the number of flowers in a bouquet, and the number of books in a library.
Integer numbers
The set of whole numbers includes the natural numbers and their symmetric numbers. This includes positive integers, zero, and negative integers. Negative numbers are denoted by a "minus" sign (-). It is designated by the capital letter Z and is represented as:
A symmetric number is one that added with its corresponding natural number gives zero. That is, the symmetric of n is -n , since:
Positive integers are numbers greater than zero, while numbers less than zero are negative integers.
Integers are used to:
- represent positive numbers: gains, degrees above zero, distances to the right;
- represent negative numbers: debts, losses, degrees below zero and distances to the left.
Examples
At the North Pole the temperature is below 0ºC for most of the year, between -43ºC and -15ºC in winter. A person buys a vehicle for 10,000 pesos but only has 3,000 coins.
This means that he owes 7,000 coins.
Rational numbers
Fractional numbers arise from the need to measure continuous quantities and inaccurate divisions. Measuring continuous quantities such as length, volume, and weight, prompted the man to enter fractions. The set of rational numbers is designated by the letter Q:
Examples
A cake divided by three people is represented as 1/3 a third for each person; one tenth of a meter is 1/10 m = 0.1m.
Irrational numbers
Irrational numbers comprise numbers that cannot be expressed as integer division in which the denominator is nonzero. It is represented by the capital letter I .Those quantities that cannot be expressed in whole form or as a fraction that are incommensurable are also irrational. For example, the ratio of the circumference to the diameter the number ? = 3.141592…
The roots that cannot be expressed exactly by any whole or fractional number are irrational numbers:
Properties of real numbers
- The sum of two real numbers is closed, that is, if a and b ? ?, then a + b ? ?.
- The sum of two real numbers is commutative, so a + b = b + a.
- The sum of numbers is associative, that is, (a + b) + c = a + (b + c).
- The sum of a real number and zero is the same number; a + 0 = a.
- For each real number there is another symmetric real number, such that its sum is equal to 0: a + (- a) = 0
- The multiplication of two real numbers is closed: if a and b ? ?, then a. b ? ?.
- The multiplication of two numbers is commutative, so a. b = ba
- The product of real numbers is associative: (ab) .c = a. (B .c)
- In multiplication, the neutral element is 1: so, a. 1 = a.
- For each real number to different from zero, there is another real number called the multiplicative inverse, such that: a. a -1 = 1.
- If a, b and c ? ?, then a (b + c) = (a. B) + (a. C)
Origin of real numbers
The discovery of real numbers is attributed to the Greek mathematician Pythagoras. For him there was no rational number whose square is two:
![]()
So the ancient Greeks saw the need to call these irrational numbers .
Luke is passionate about fostering student involvement and connection. He studied psychology for his major and likes learning about the past. Luke aims to specialize in artificial intelligence and cybersecurity. .